Chandrasekhar limit is the maximum possible mass of a stable cold star, above which it must collapse into a black hole.

In the year 1928, an Indian graduate student named Subramanian Chandrasekhar who went to Cambridge University to study astronomy, stumbled upon a revolutionary idea about stars. The young Indian scholar thought that it would be intriguing to know how big a star could get while still supporting itself against its very own gravity even after it has used up all of its fuel that illuminated itself at the first place. It is understood that, in its lifespan, when a star eventually becomes very small, the matter particles in it becomes very close to each other. And based on Pauli Exclusion Principle, these particles have very different velocities which make them move away from each other which, in effect, make the appearance of the star as if it is expanding. And thus, a star, at that stage, maintains a steady radius given the balance that exists between the attractions of gravity and the repulsion that arises from that very exclusion principle. But Chandrasekhar very soon realized that there's got to be a limit to the process of repulsion that the exclusion principle provides.
It is understood that according to the law of Theory of Relativity, given nothing could travel faster than the speed of light, there is a limit to the maximum differences in the velocities of the matter particles in the star. And as per this understanding, when the star is sufficiently dense, the repulsion rate triggered by the exclusion principle would be less than the attraction of the gravity. And the brilliant Tamil scientist calculated that a cold star of more than one and half times the mass of our very own Sun would not be able to support itself against its own gravity. And this mass is now known as the Chandrasekhar limit.
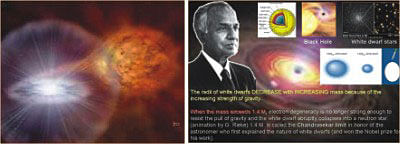
Let's understand this in stellar terms. Most stars in the Cosmos end their lives as white dwarfs (WD) and the size of such WD depend on its mass. And unlike other stars, WD shrinks in sizes as their mass increases and a WD as massive as our Sun will have a diameter like that of the Earth. And with greater mass, WD gets smaller and smaller while the rate of WD density increases progressively side by side. And at 1.4 solar masses (more than one and half times the mass of our very own Sun, as previously discussed) the WD come to its smallest possible diameter limit and this critical limit is called Chandrasekhar Limit. At this stage densities of the WD would weight hundreds of tons per cubic inch where electrons drive into protons in the nuclei of atoms which effectively produce neutrons and eventually a neutron star is formed out of the whole process.

The contributor is a freelance science writer.